The power of valves for better flow control, improved reliability & lower expected payment failure rates on the Lightning Network

Writen by BitMEX Grantee Rene Pickhardt

Abstract: Valves are an important tool for flow control in fluid or gas networks. We investigate the possibilities to set up valves on the Lightning Network to improve flow control and reduce expected payment failure rates. We show that good asymmetric choices for `htlc_maximum_msat` on a channel can reduce the expected payment failure rate significantly. We assume that the potential benefits from carefully selecting `htlc_maximum_msat` as a valve seem not to be fully exploited by routing node operators and Lightning Service Providers yet to optimize their flow control and improve the reliability of their channels. We analyze the power of valves on the Lightning Network mathematically by using Markov Chains. These can be used to model the uncertainty about the liquidity in a channel that arises from drain in the depleted channel model. Using these techniques we show theoretically that properly using valves may statistically lead to a more balanced channel and expected payment failure rates drop from two digit numbers below 3%. We provide two experimental algorithm ideas and encourage Lightning node operators to investigate the potentials from utilizing this tool that is already being shipped with the protocol. 

Introduction & Motivation

As we know payments on the lightning network correspond mathematically to (minimum cost) flows and Lightning Service Providers have liquidity as a major topic to achieve a reasonably high service level objective. Furthermore it is well known that channels frequently deplete. Depletion occurs when more sats are supposed to be sent in one direction than in the opposite direction (A phenomenon that is usually referred to as drain). As we have discussed in this blog, depleted channels and even small drain values are a major source of expected double digit payment failure rates and reduced reliability of the network.

Currently Lightning Node operators engage in liquidity management and mainly try to mitigate the problems arising from drain of channels via the following two strategies: 

1. Refilling the depleted channel: Several techniques are known to refill the liquidity. The node operator could make a circular payment or make an off chain swap. Furthermore the channel could be closed and reopened or an unannounced parallel shadow channel may exist. Future improvements to the protocol might also allow the possibility to splice new liquidity into the channel. Particular to all of these mechanisms is that they are costly for the node operator.Furthermore, globally there are only limited possibilities to conduct such operations using onchain transactions as blockspace is scarce and Mempool congestion spikes might significantly not only put a higher cost to such strategies but also put a delay to them.   
2. Reduce the drain / find balanced channels: Tools like CLBOSS try to adopt the routing fees a node charges on its channel with respect to the drain. The philosophy is mainly boiling down to an economic argument: If there is drain on a channel that one operates this means there is demand for that liquidity so increasing the routing fees would on one end increase the revenue while on the other hand potentially lower the demand and decrease the drain. Following a similar philosophy protocol developers suggest adding negative fees and various fee rate cards to the protocol. Other strategies that operators put effort into is to carefully select peers and predict where their liquidity may be needed or flow in a balanced way. Entire proprietary ranking and scoring systems for nodes exist to support node operators in their decision making. 

In this article we will see that there seems to be a third and very promising strategy to establish better flow control (liquidity management) that is already baked into the protocol namely the `htlc_maximum_msat` field in the `channel_update` message. We demonstrate that `htlc_maximum_msat` can and should operate as a valve to achieve flow control. Looking at the recent channel policies on the gossip protocol, we note that currently almost all channels have either `htlc_maximum_mset` set to their channel capacity or have the same value in both directions. We will show that both settings are undesirable as they tend to amplify the depletion of channels with a given drain. Given these statistics we assume that as of writing almost no nodes actively make use of the opportunities that we propose and discuss in this article. 

Let us start with an openly licensed (CC-BY-SA 4.0) quote from the Wikipedia article about valves to get the right mind set and metaphors for us: 

A valve is a device or natural object that regulates, directs or controls the flow of a fluid […] by opening, closing, or partially obstructing various passageways. […] In an open valve, fluid flows in a direction from higher pressure to lower pressure. […] Modern control valves may regulate pressure or flow downstream and operate on sophisticated automation systems. […] Valves have many uses, including controlling water for irrigation, industrial uses for controlling processes, residential uses such as on/off and pressure control to dish and clothes washers and taps in the home. 

As a valve `htlc_maximum_msat` theoretically has the potential to significantly reduce expected payment failure rates in the network and produce balanced channels. 

Before continuing to explain how `htlc_maximum_msat` acts as a control valve, one important side note on balanced channels: There is the widespread misbelief that a channel is balanced if 50% of the liquidity belongs to each peer. We have shown that 50/50 channels are not desirable and practically also almost impossible to both achieve and maintain. One can think of the myth of Sisyphus where one might rebalance a channel towards a 50/50 balance just to realize that there is drain on the channel and the channel depletes again. Thus A better definition for a balanced channel would be to define a channel to be balanced if and only if the liquidity distribution is close to a uniform distribution. As shown the distribution of channels with drain seems to follow an exponential curve, which is certainly far away from a uniform distribution.

`htlc_maximum_msat` as a valve to mitigate the depletion of liquidity on payment channels with (high) drain

Recall from the wikipedia quote that  “Modern control valves may regulate pressure or flow“. The equivalent to pressure for a payment channel would be its drain. We define Alice’s drain on her channel with Bob as the fraction of payments that Alice is supposed to forward to Bob in comparison to all payment requests that occur on the channel. A drain value of 0.9 would mean that if 10 payment forwarding requests are made on the channel 9 of them ask Alice to forward sats to Bob. At the same time only one payment request asks Bob to send sats in the direction of Alice. For a short moment we assume all payments to be of equal size. It is easy to see that because of the pressure coming from the drain most of the liquidity will be on Bob’s end of the channel very quickly. This will also result in the fact that Alice will not be able to fulfill most of the payment routing requests. This can be measured and observed during operation as a high payment failure rate on the channel.

Since we can think of drain on the channel as pressure and knowing from the real world that the flow through a network can be regulated by a control valve we should look out for such a valve on the Lightning Network. If one expects 9 out of 10 payments to go from Alice to Bob an obvious measure that Alice can take to reduce her failure rate on the channel is to decrease the size of the payments that she is willing to forward and limit the liquidity that is being drained from the channel while fulfilling the payment requests. This can be done by announcing a lower `htlc_maximum_msat` value via a `channel_update` on the gossip protocol (See the discussion section for limitations with this coming from implementations). This effectively lowers the throughput of the channel from Alice to Bob. The exact value has to be learnt during operation or can – like we show – be theoretically estimated given some assumptions about the payment size distribution. Selected carefully the drain may persist and the `htlc_maximum_msat` might be more stable and controlling the flow may result in a more stationary process than fiddling around with routing fees.

The following is to the best of our knowledge the first mathematically sound description and analysis that explains the effect and power of control valves on the Lightning Network. While a vast majority of nodes currently seems to ignore the potential of using `htlc_maximum_msat` as a valve, we note that the idea to use `htlc_maximum_msat` is not new. Some operators have been playing with the idea to signal via `htlc_maximum_msat` how much liquidity they may have available or left in the channel. For example on the gossip protocol it is notable that zerofeerouting has times where some of the channels have a very low `htlc_maximum_msat` value. This behavior effectively deactivates routing on the channel in the direction of the drain by closing the valve and allows the channel to undeplete before the valve is being opened again. While this seems to be a drastic measure for flow control the principle of utilizing this field as control valve is already in place.

With all this motivation and intuitive description let us dig into the mathematics of a payment channel to study the potential of using valves with the goal to achieve a better flow control: 

The Markov Process for describing the uncertainty about the Liquidity in a payment channel with a given drain. 

Let us assume we have a channel with capacity `c` between Alice and Bob. This means that at any given time Alice can have a liquidity of 0,1,…,c-1 or c satoshis in the channel. As usual we ignore for simplicity of presentation the channel reserves and considerations about in-flight htlcs. We model the sats that belong to Alice as a state of a finite Markov process. The Markov process has c+1 states as Alice can have any of those values as her liquidity. 

For a short moment we make the strong simplifying assumption that payments on a channel can only be of size 1 satoshi. 

If Alice has `a` sats of liquidity the Markov process would be in state `a`. Additionally we take the drain of the channel as the fraction of payments that Alice is supposed to route to Bob in relation to all payments that are requested to be routed on the channel. 

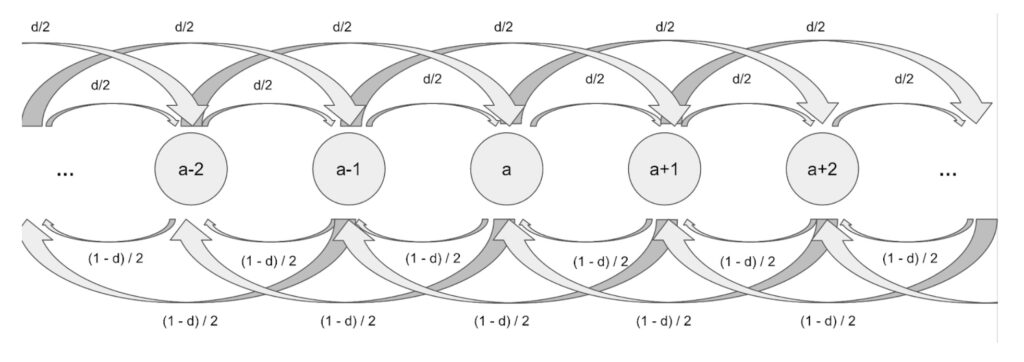
This means that we have the following two transition probabilities for any value of a between 1 and c-1. 

P(X=a-1| X=a)=1-d

P(X=a+1|X=a = d

We can look at this visually with the following diagram:

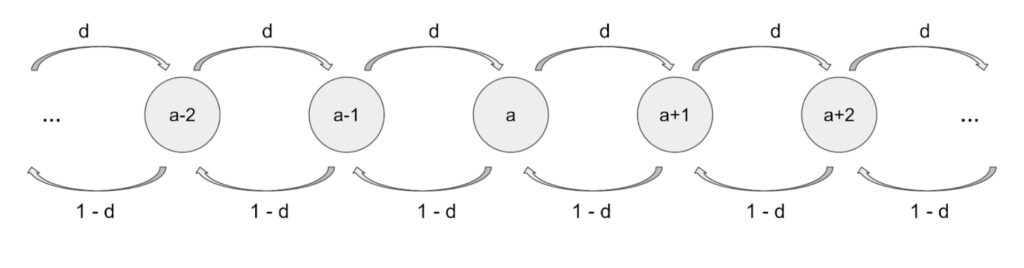
If the channel was of infinite capacity we could model this as a random walk. However on the Lightning Network the capacity of channels is finite and thus we have to look at what happens with the Markov chain as soon as we hit the limits of the (depleted) channel. In such cases the payment cannot be forwarded and the state does not change. In math formulas this means:

P(X = 0 | X = 0)= 1 – d

P(X = c | X = c) = d

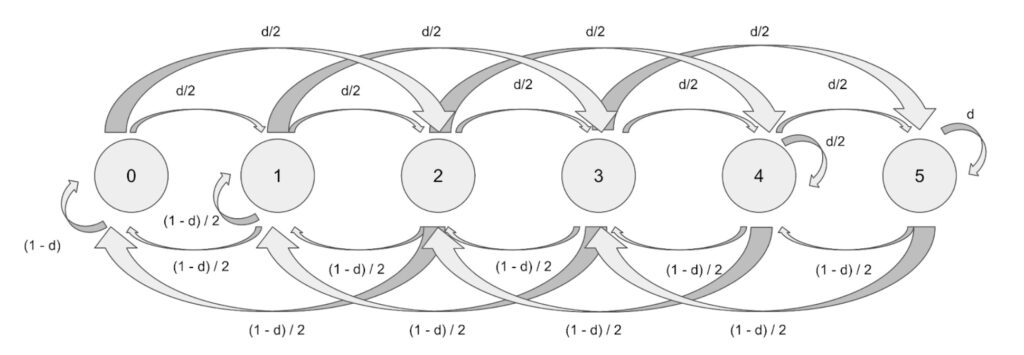
Which can visually for a channel of capacity 5 look like the following diagram.

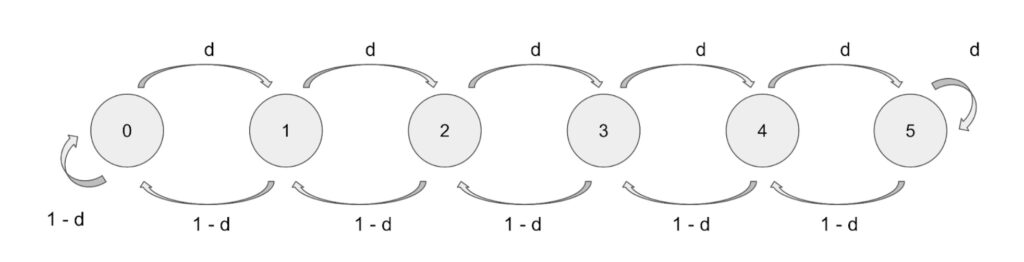
Note that the only difference is in State 0 where Alice has no sats and where the probability to stay in the state equals `1-d` and state `c=5` where Alice has `5` sats and the probability to stay in the state equals the drain `d`. 

Steady State and stationary vector of the Markov Process

The main question with respect to Markov processes is how likely is it to be in a given state if the process runs long enough. In the case of the Lightning Network this translates to the question: “Given a fixed drain and channel capacity and only 1 sats payments: How likely is it that Alice has eventually x sats of liquidity?”

From math we know that we can compute this rather easily. So let us assume we have a vector space of dimension `c+1` with each state of the Markov process (potential liquidity value of Alice) as a base vector  and a stochastic mapping that encodes as a transition matrix in the same way as described. This would result in the following transition matrix for a channel of 5 sats capacity

We note that this is a tridiagonal matrix. We will describe later how larger payments will lead to a band matrix. Without formal proof we can see that for drain values other than 0.5 the Markov process should not oscillate but converge into a steady state. It is easy (but computationally very inefficient) to create a small program which raises the power matrix to a very high power and evaluates any initial state vector multiplied with the high power of the matrix. This results in a stationary state which encodes the uncertainty encoded in the liquidity distribution. 

In particular this Markov process results in the same liquidity distribution as the simulated constrained random walks that we have previously used to estimate the liquidity distribution of a channel as can be seen in the following diagram: 

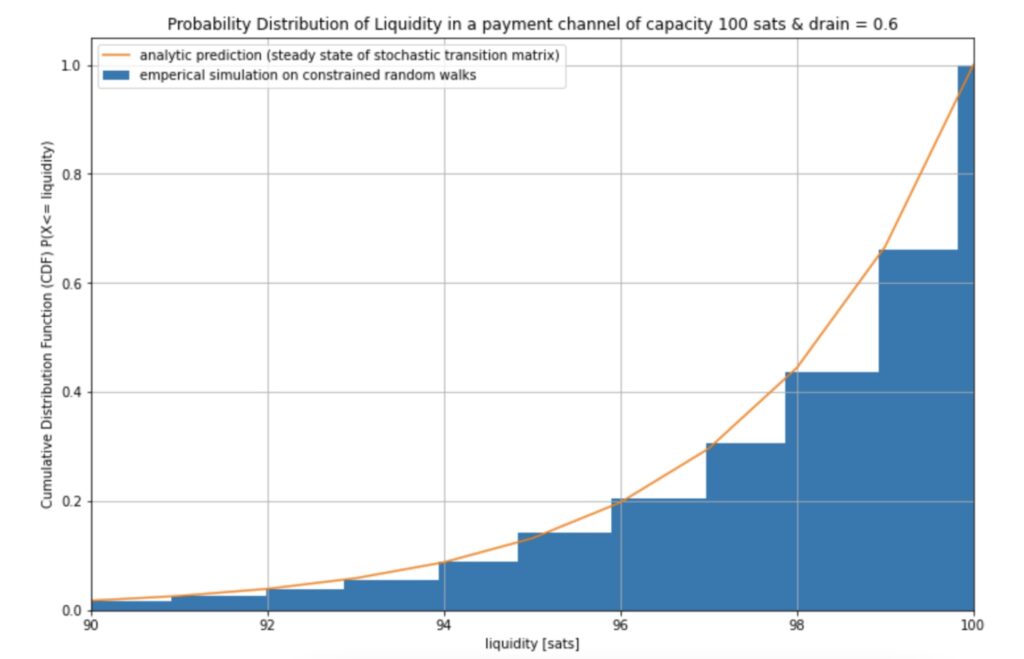
Of course in practice we can do a bit better than the naive approach of computing a high power of the matrix. As the steady state does not change the state vector `v` (which encodes the liquidity distribution for Alice) we can just solve the system of linear equations given by `v= vM` under the constraint that the sum of all components of `v` has to be `1`. This is equivalent to solving (MT – I)vT = 0. The resulting vector `v` describes in each component how likely it is that the state of the Markov process is taken.

Varying the Parameters of the Markov Process

We identify 3 main parameters for the Markov process: 

1. The capacity of the channel which is 1 less than the dimension of the vectors space
2. The drain of the channel which corresponds to the transition probabilities
3. The `htlc_maximum_msat` (and the distribution of payment sizes) which we have artificially set to 1 in the above example. 

The main limitation of the above consideration was that we set the `htlc_maximum_msat` to one and allowed only 1-satoshi payments. This can be resolved in various ways. We present one fairly reasonable generalization. To understand the gist let us look at the 2-satoshi case and assume that the various payment sizes (1 sat and 2 sats) are uniformly distributed and thus equally likely to occur for a given payment routing request. This assumption can be dropped by designing the Markov chain differently. For example in our code we also looked at zipf distribution as it seems more likely for payments to be small. In any case to show how everything works it is easiest to explain the concepts using a uniform payment size distribution. 

For a given drain of `d` and for a state `a` we now have two transition probabilities:

P(X=a+1 | X = a) = d/2

P(X = a+2 | X = a) = d/2

This is because for the two satoshi case we either send 1 satoshi or 2 and both probabilities have to add up to our drain `d`

In the opposite direction we consequently get: 

P(X=a-1 | X = a) = (1-d)/2

P(X = a-2 | X = a) = (1-d)/2

As in the 1 satoshi case we have to take caution when the channel depletes. Since we allow payments of size up to 2 this can happen for example in state 0 and 1. So we get: 

P(X = 0 | X = 0) = 1-d         # a 1 or a 2 sats payment was requested in state 0

P(X = 0 | X = 1) = (1-d)/2    # a 1 sat payment was requested in state 1

P(X = 1 | X = 1) = (1-d)/ 2  # a 2 sat payment in state 1 was requested which cannot be fulfilled

This results in the following diagram:

Setting q = (1-d) we can again look the matrix representation of the process: 

Similarly we could create larger chains for channels with higher capacity or band matrices with more bands for higher `htlc_maximum_msat` values. The lnresearch repo on github contains a notebook with code that can do this and compute the resulting stationary distributions for you.

In particular we can set a different `htlc_maximum_msat` in the direction of the drain than in the opposite direction. Recall from our motivating example with a higher drain that we want to limit the allowed payment size in the direction of the forwadings. So please have a look at the diagram that shows the Markov process in which Alice sets her `htlc_maximum_msat` to 1. At the same time Bob keeps his at 2 since both Alice and Bob expect more payment routing requests for Alice than for Bob, but wish to maintain a balanced channel that should not drain: 

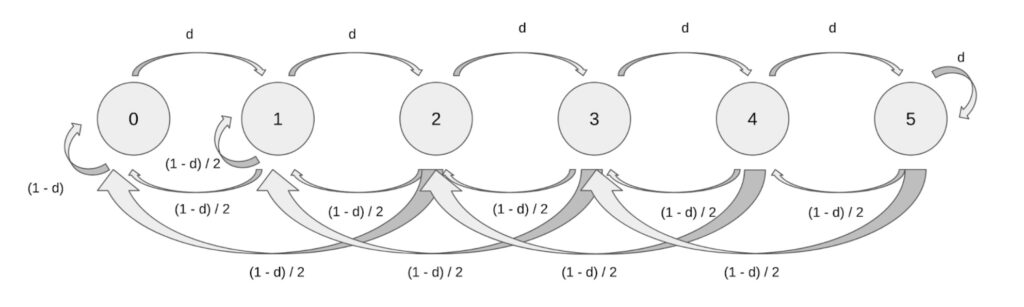
The corresponding transition Matrix looks like the following. 

 

We can of course generalize this to arbitrary values of `htlc_maximum_msat` for Alice and for Bob. The `htlc_maximum_msat` for Alice encodes how many bands are used above the diagonal and the `htlc_maximum_msat` for Bob encodes how many bands are used below the diagonal. 

For a given drain we search for a Markov process for which the expected payment failure rate of the steady state vector on the channel is minimized. 

While the payment size distribution and its change when adopting the `htlc_maximum_msat` value can only be learnt during operation of a node and with actual data, we continue our theoretical observations. Thus, in the next section we look at how to compute expected payment failure rates. 

Compute expected payment failure rates on channels with uncertainty about the liquidity (potentially arising from drain)

Once we have a probability distribution – which may or may not be derived from the depleted channel model that comes from drain – encoding the uncertainty about the liquidity, we can compute the likelihood for a payment of size `a` to fail via the following formula: 

failure_rate(a) = drain*P(X>c-a) + (1-drain)*P(X<a)

One can easily understand this by realizing that a payment of size `a` will fail in two cases.

1. If it is against the direction of the drain and the channel has less than `a` sats of liquidity available. The probability for this to happen is computed as (1-drain)*P(X<a)
2. If it is in the direction of the drain and the channel partner has more than `c-a` sats of liquidity. The probability for this to happen is computed as `drain*P(X>c-a)`

The sum of both probabilities is the expected failure rate for a payment of size `a` as described above.

The average expected failure rate is the average over all possible values of `a` which may be weighted, if we assume that the amounts are not equally distributed. In any case the payment sizes are limited by `htlc_maximum_msat` so we can compute the expected payment failure rate via:

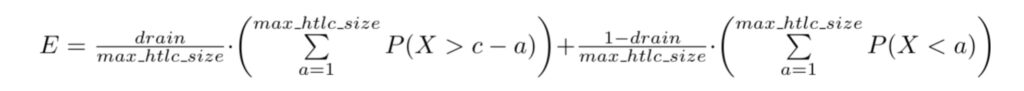
This assumes the same `htlc_maximum_msat` in both directions and we can see how the expected payment failure rate changes a bit by varying the setting. In particular we see that stronger drain requires higher `htlc_maximum_msat` values to minimize the expected payment failure rate.

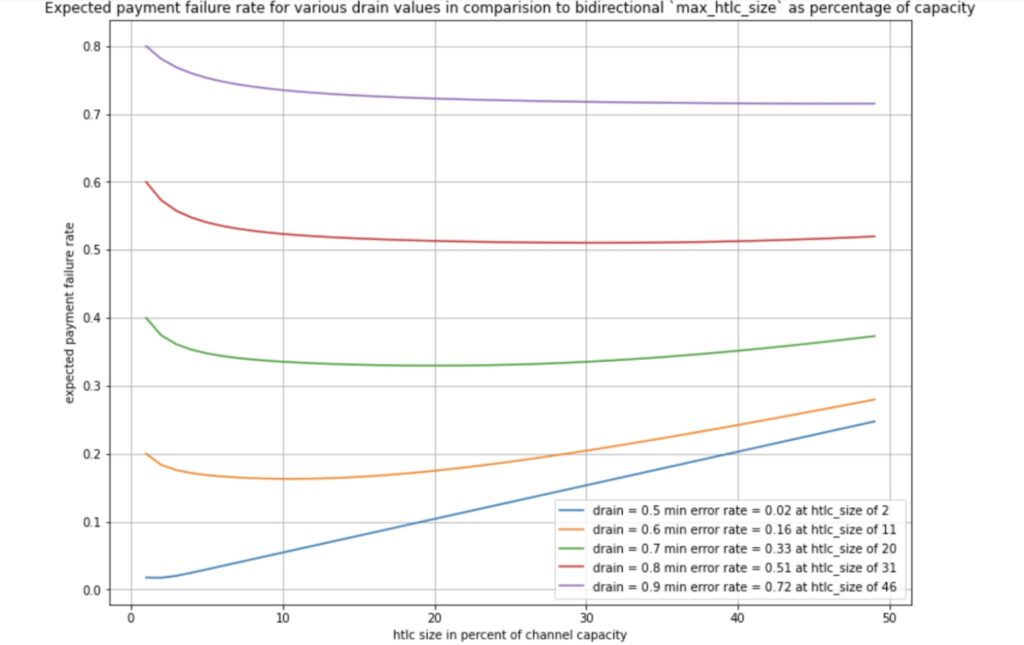
We can see that when increasing the `htlc_maximum_msat` for a given drain the expected error rate drops when increasing the `htlc_maximum_msat` to its minimum and then starts to increase again. However we can note that unless we are in a scenario with hardly any drain the change of `htlc_maximum_msat` does not seem to significantly help to reduce the error rate.

However if we assume asymmetric values for `htlc_maximum_msat` where Alice sets `htlc_maximum_msat_A` for the maximum number she is willing to forward and Bob does the same via `htlc_max_size_B` we get the following formula for the expected failure rate and a two dimensional optimization problem which Bob and Alice have a mutual interest to solve for a given drain.

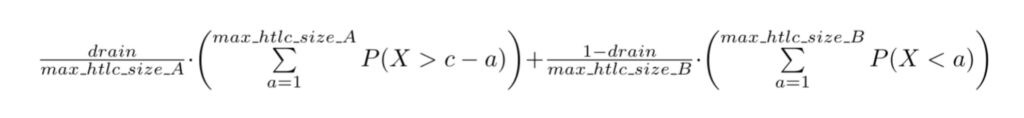
The motivation for studying this is quite simple. Assume you have a channel with a drain of 0.75 from A to B. This means that statistically 3 out of 4 payments go from A to B while only one payment goes from B to A. If node operators would now rate limit the throughput of payment sizes in direction from A to B to a fraction of what is allowed to be routed from B to A then statistically the channel would stay balanced and thus reduce the expected payment failure rate. For drain values up to 0.95 we have computed the optimal `htlc_maximum_msat` pairs and depicted the expect payment failure rate in the following diagram: 

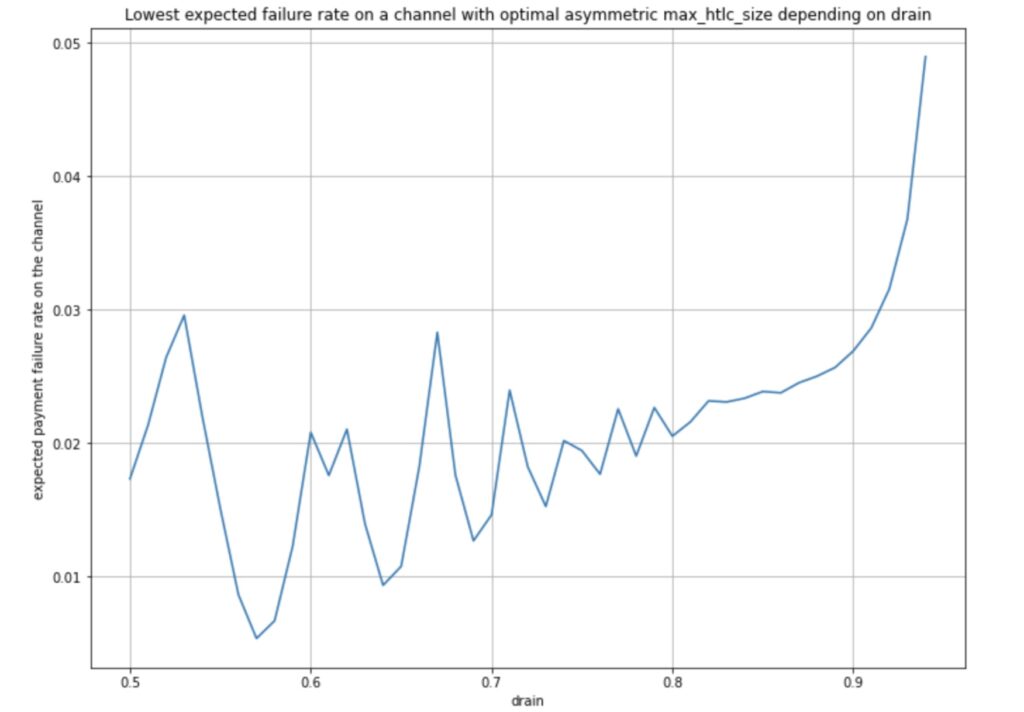
We can observe that for drain values up to 0.90 (meaning 9 of 10 payments flow in the same direction) the expected payment error rate drops to below 3%. This is quite some improvement. Assuming all drain values occur equally often the median failure rate is now 2.18%. This is a stark improvement when we realize that this value was 40.88% if the channel used the same `htlc_maximum_msat` value in both directions. As expected, failure rates increase drastically for drain values close to 1 and the improvement when looking at averages is not so strong. The average expected failure rate of payments over all drain values is 5.43% when optimal values for `htlc_maximum_msat` are being chosen in both directions. This is still quite some improvement from the 43.1% if the `htlc_maximum_msat` value was chosen to be equal in both directions.

We can also see how the distribution of the liquidity tends to become much closer to the uniform distribution: 

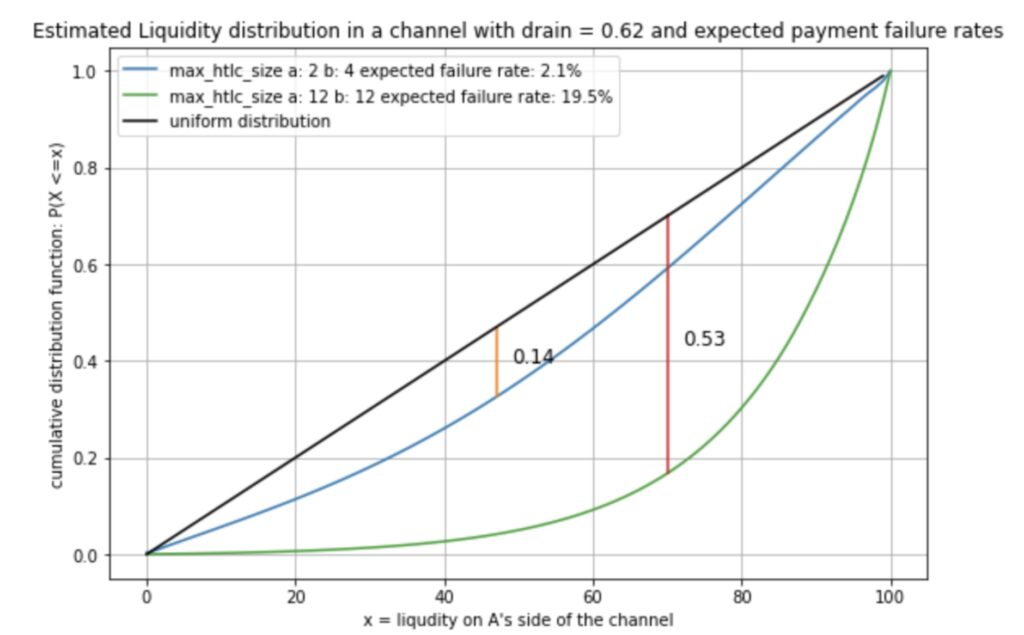
While the green curve becomes more skew for larger drains we can see that the blue curve would always stay closer to the uniform distribution of liquidity and thus a balanced channel and lower failure rates.

Of course one should be careful about the results. We don’t know the precise payment amount distributions and how they would change if node operators start to establish flow control via this parameter. This would change the Markov model and the weighting in the optimization problem. Assuming different parameters we have however observed similar effects. In particular we have not investigated the dynamics if this is occurring on the entire network and we have not tested this in practice yet, but invite node operators to do so and share their experience or reach out and work together with us to test this.

It seems as if a large number of node operators are currently not aware of the importance purposefully choosing  `htlc_maximum_msat` . As of writing this article 73.1% of all channels use the same `htlc_maximum_msat` value in both directions. As discussed in this article this predicts overall higher failure rates and demonstrates that there are unused potentials by node operators to improve flow control, increase network reliability and decrease expected payment failure rates. 

An important side note: I often criticized some developers privately who used `htlc_maximum_msat` instead of capacity during payment delivery in order to compute candidate onions. I think from a min cost flow perspective we should use `htlc_maximum_msat` as the capacity of the arcs of the min cost flow problem to plan our payment. We can still use the actual capacity (sorry for the same word but different semantics!) of the channel to estimate our cost function. That being said, there seems to be quite some merit in actually using `htlc_maximum_msat` as the liquidity limitation of a channel during payment delivery and computation of candidate onions. So sorry to the devs whom I criticized in the past for doing so. 

Discussion: Limitations & Opportunities of the Model

The presented model has – as any model – some severe limitations and shortcomings and does not match the reality. To create the markov chain we assume to know the drain of a channel and the distribution of payment sizes between 1 sat and the `htlc_maximum_msat`. While both may potentially be estimated during node operations, these assumptions could change dynamically. In particular  a change in the `htlc_maximum_msat` may also change these assumptions for the model. So you could ask how useful the model is? Well it helps us in a controlled setting to understand and see the effect of valves and draw conclusions about their potential. At the end of our notebook we provide 2 experimental algorithms that node operators could use or adopt to find good values for the `htlc_maximum_msat` value. In Particular we have one algorithm in which a node operator does not have to create a markov chain. The idea is to build a liquidity distribution in the channel of the last 10k payments and measure how far this distribution is away from the uniform distribution. As explained before, if the distribution is far from the uniform distribution this may be an indicator that we have a drain and a potentially a depleted channel. In such cases adopting the `htlc_maximum_msat` value can mitigate this (as motivated through the Markov Model). This is particularly useful as a node operator can obviously know the liquidity distribution of the last k payments. The operator does not need to know the drain on the channel or the payment size distribution in order to measure a signal to change `htlc_maximum_msat`. Thus, while the model has the typical limitations of a model it leads node operators to easy strategies which can be used to adopt their settings.

Of course node operators have to test on mainnet if changing `htlc_maximum_msat` is useful and indeed improves the reliability by a reduction of the expected payment failure rate on their channels. From the Markov Model we can see that lower `htlc_maximum_msat` values yield lesser variance and thus a lower expected payment failure rate. Of course in reality we don’t want to select this argument to be  arbitrarily low. So again node operators will probably have to make some trade-offs here. While we suspect that the `htlc_maximum_msat` pair per channel may be rather stable it is not clear how often it will need to be updated. The gossip protocol of course only allows on average for 4 updates per day. Also some people with whom we have discussed the ideas of this article pointed out that there may be privacy implications. Of course node operators would implicitly signal drain on their channels with the world if they started to use the `htlc_maximum_msat` pari as a valve. This may of course be interesting for competing routing nodes as they could now understand where liquidity may be needed. While this could overall be good for the network’s reliability it may not be of interest for node operators to educate their competition. Assuming this is not an issue we note that operators of a channel seem to have mutual interest to find a good `htlc_maximum_msat` pair on their channel and adapt it during operation if the drain on the channel changes. We note that the opportunity to use valves happens on a per channel base and does not need network wide adoption.

Warning: We note that according to BOLT 7 the semantics of `htlc_maximum_msat` is currently a bit vague. Bolt7 reads: A node “SHOULD consider the htlc_maximum_msat when routing“. However many implementations currently split the amount in some way and try to deliver partial shards by solving a path finding problem on the network where all channels have a larger `htlc_maximum_msat`. This of course may remove channels where the value is too small, which in turn would remove some of the drain. If implementations would use min cost flow solvers by default they would most likely take the offered liquidity and not change the drain. While for the theoretical model this may lead to some inaccuracy we suspect with the presented algorithms that this will not be a problem in practice. 

Conclusion

We have seen how for a given drain on a channel choosing an asymmetric pair of `htlc_maximum_msat` may significantly reduce the expected payment failure rate of a channel. A network wide adoption is expected to improve the overall reliability of the network. At the same time channels that use `htlc_maximum_msat` as a valve tend to be more balanced. Even with high drain channels we see their liquidity distribution is closer to the uniform distribution than a channel without this flow control measure. On the Internet flow control is done by the sliding window mechanism of the Transmission Control Protocol to address some of the reliability issues of the Internet protocol. While the `htlc_maximum_msat` might make one think of the window_size in TCP it is a Lightning Network native parameter to work towards better flow control. Other Lightning Network native parameters to improve flow control may exist and be identified in the future. While we hope that node operators can already just selfishly choose their `htlc_maximum_msat` following the ideas from our provided algorithms, we note that an interactive communication protocol to find the pair of `htlc_maximum_msat` values may be necessary to automate the process of flow control on a protocol level. 

On a personal note: People who have been following my work more closely know that during 2022 after I have described the depleted channel model I have become rather critical and skeptical if the Lightning Network could ever reach the desired service level objectives. With the current results I have become hopeful again that there is more potential that we have overseen and that the Lightning Network could in fact reach the desired service level objectives. In any case I am still confident that we will need a mechanism to have redundant overpayments as well as other tools and mechanisms to improve the reliability of the protocol.

Acknowledgements

Thank you to Stefan Richter for helpful and critical discussions about earlier ideas and versions of this text and to Andreas Antonopoulos for encouraging me to expand on the motivation section and help me select proper analogies to explain the workings of doing flow control via `htlc_maximum_msat`. Special thanks to zerofeerouting for notifying me while I had discussed preliminary results with him that he already uses `htlc_maximum_msat` as a valve. Christian Decker and Anoine Riard also provided very helpful feedback and critical review for which I am grateful. Finally Summer of Bitcoin allowing research projects and the discussion with my mentees gave me quite some inspiration to derive the liquidity distribution of channels with drain from Markov chains. In that context I thank Sebastian Alscher for stylistic proofreading. Of course I am grateful to everyone who supports my open source research!  

Related

The post appeared first on Blog BitMex